A Distribuição Espacial do Índice Espectral

Um dos objetivos principais, senão o mais importante, na prepara-ção de mapas de céu inteiro é nterpretar o padrão espacial da emissão Galáctico em função de seu espectro. Esta questão é de particular interesse para o componente síncrotron, dado que sua emissividade depende, como veremos a seguir, tanto do fluxo de elétrons relativísticos quanto da intensidade do campo magnético numa dada região da Galáxia. Nesta seção elucidaremos a associação entre as propriedades do meio interestelar e o comportamento espectral da emissão síncrotron.

Mas antes de particularizar nossa abordagem sobre esta questão convém definir os processos de radiação que caracterizam a emissão Galáctica como um todo. Esta se compõe de:

(a) Radiação síncrotron emitida por elétrons relativísticos espiralando no campo magnético B da Galáxia, cuja intensidade

recebe as contribuições da potência espectral P ∝ B^(p+1)/²ν^-(p-1)/2 de cada elétron de massa m_c e carga q na freqüência ν ao longo do percurso l até o observador segundo um espectro de energias N(E)dE = k(1)E ^-pdE, tal que se k' ≡ k(m_ce²)^1-p e C_ijk ≡ q^k / mⁱ_ec^j (c é a velocidade da luz), então

sendo que para uma distribuição isotrópica de alinhamentos entre B e o campo de velocidades dos elétrons

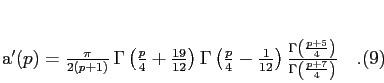
(b) Radiação Bremsstrahlung térmica, ou livre-livre, produzida pelo gás ionizado quente (temperatura eletrônica Τ_e = 0,6 - 1,0 × 10⁴ K) e de baixa densidade (n_e ≈ 0,3cm ^-3) do meio interestelar com intensidade

Sendo K a constante de Boltzmann e g₁₁(Τ_e, ν) o fator de Gaunt. Num meio ionizado predominantemente composto de HII (Ζ = 1, n_HII ≡ n_i = n_e), e opticamente fino, o cálculo detalhado do fator de Gaunt mostra que g₁₁ = (√3/π) P₁, sendo P₁ e ln(P₁/P₂) e os limites inferior e superior do parâmetro de colisão entre os elétrons e os íons. O correspondente índice espectral entre as freqüências ν₁ e ν₂ (ambas em GHz) resulta em

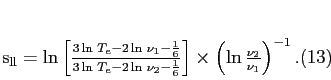
(c) Radiação térmica da poeira, que emite como um corpo cinza à temperatura Τ_cc com intensidade

sendo que a integral do coeficiente de absorção α(ν, 1) é a opacidade do meio (≪ 1) e B_ν é a função de Planck.

A Figura 8 mostra a relação de intensidades em unidades de temperatura de antena entre estes componentes e um corpo negro com a temperatura da Radiação Cósmica de Fundo (para maiores detalhes, veja a seção 1.3.2).

Figure: Espectro dos componentes da emissão Galáctica comparado com o da RCF entre 408MHz e 1.000GHz. A largura das respectivas bandas evidencia a variação esperada dos componentes Galácticos com a latitude 15° ≲ |b| ≲ 70° segundo um modelo de camadas plano-paralelas em relação ao Plano Galáctico.

Observacionalmente, o espectro do componente não-térmico se torna mais inclinado com a freqüência. Webster (1971) mediu o espectro da emissão Galáctica em regiões próximas ao Pólo Norte Galáctico ( b > 70° e b > 50° para 50° < l < 90° e b > 30° para 70° < l < 90°) e ao anticentro Galáctico (15° < b < 50° para l = 180° ± 40° ) que se identificariam com emissões características da região intermediária entre braços espirais da Galáxia (com aproximadamente metade da emissão proveniente do halo) e do braço espiral local, respectivamente (Figura 9). Os dois espectros mostram uma variação no índice s ≡ (p - 1)/2 da Equação (4), tal que ^s(ν ≲ 200MHz) = 0,4 e ^s(ν ≲ 400MHz) = 0,8 - 0,9.

Figure: Espectro da emissão Galáctica nas regiões do anticentro (I) e do Pólo Norte Galáctico (II). As unidades no eixo da intensidade são 10-17 ergs -1 cm -2 Hz -1 sr -1 ou, equivalentemente, ≃ 3,25 × 105K (Fonte: Adaptada de Longair (1994a), p. 263).

Kallas et al. (1983) utilizaram o mapa de Haslam em 408MHz e e mais dois mapeamentos parciais do Hemisfério Norte, o de Berkhuijsen (1972) em 820MHz e o de Reich (1982) em 1420MHz, para investigar a distribuição do índice espectral na região do anticentro Galáctico entre Cassiopéia e Perseus. Após convoluirem os mapas em 408MHz e 1420MHz para a resolução de 1,2° do mapa de Berkhuijsen, eles extraíram o componente do contínuo isento de fontes discretas e de esporas e constataram que esta região apresenta um espectro com uma inclinação acentuada. Denotando de β_{[ν1, ν2]} o índice espectral determinado entre as freqüências ν₁ e ν₂, eles encontraram índices médios β_[408,820] = 2,70 ± 0,50, β_[408,1420] ∼ 2,85, β_[820,1420] ∼ 3,05. Como o índice espectral das regiões isentas de estrutura no padrão espacial do contínuo não-térmico (componente de fundo em grande escala) é ≈2,7, sua filtragem permitiu, ainda, identificar um componente de espectro com β_[408,1420] ∼ 3,1 e β_[820,1420] ∼ 3,5. Em termos do mecanismo de radiação síncrotron, a constituição do meio interestelar na vizinhança solar se mostra, como veremos a seguir, particularmente atraente para explicar esta peculiaridade do espectro.

Carlos Alexandre Wuensche - Criado em 2005-06-02