Introdução
Nas últimas décadas temos percebido um aumento rápido no conhecimento sobre a nossa vizinhança cósmica e, com as observações de objetos cada vez mais distantes, a fronteira do Universo parece ter sido empurrada para os confins do tempo. Somos a primeira geração de seres humanos capazes de perceber os grandes detalhes da História Cósmica, das origens do Universo até o desfile das estrelas vizinhas ao nosso próprio Sol.
O chamado Modelo Cosmológico Padrão (MCP), ou ΛCDM, é o modelo atualmente aceito para descrever a dinâmica e evolução do Universo. O arcabouço teórico considera que ele é adequadamente descrito pelas equações de A. Einstein, na forma colocada por A. Friedmann e G. Lemaitre, e sua métrica obedece a forma de Robertson-Walker (H. P. Robertson e A. G. Walker) perturbada. Ele considera que o Universo foi criado a partir de uma singularidade, há cerca de 14 bilhões de anos, e é constituído de fótons (Ωγ = ργ/ρ0), neutrinos (Ων = ρν/ρ0), bárions (Ωb = ργb/ρ0) e os chamados componentes "escuros": as chamadas Matéria e Energia Escuras (Ωb = ρc/ρ0 e ΩΛ = ρΛ/ρ0); Ωi é o parâmetro de densidade para os diferentes componentes, calculado em função de ρ0, a densidade crítica do Universo, cujo valor é da ordem de 10-29 g.cm-3. Elétrons possuem massa muito baixa e, devido à neutralidade elétrica do Universo em escalas cosmológicas, não entram neste cálculo.
As grandes estruturas do Universo (aglomerados e super aglomerados de galáxias) foram formadas a partir da evolução de flutuações de densidade de origem primordial, causadas principalmente pela interação gravitacional entre a matéria escura e bariônica. O MCP considera também um espectro inicial de flutuações de temperatura que obedece uma lei de potência, sem perturbações tensoriais, um universo espacialmente plano, uma constante cosmológica, Λ, que atua como componente de Energia Escura e uma distribuição de neutrinos cuja soma das massas é fixada em 0,06 eV.
Embora o paradigma do modelo ΛCDM seja o mais aceito, ele ainda deixa algumas questões em aberto que podem levar a novos paradigmas para a descrição do Universo. Uma delas é a confirmação do processo inflacionário que amplificou as perturbações cosmológicas primordiais e a outra é a caracterização do chamado "Setor Escuro", explicando o problema da coincidência cósmica e a origem e detalhamento de 95% dos constituintes do Universo.
Os valores dos principais parâmetros cosmológicos, obtidos a partir de medidas da Radiação Cósmica de Fundo em Micro-ondas (do Inglês, CMB) feitas pelo satélite Planck [1] em combinação com medidas de oscilações acústicas de bárions (do Inglês, BAO) ambos observáveis encontram-se na Tabela 1. Os seis primeiros parâmetros foram diretamente ajustados aos dados do Planck:
- densidade de bárions (Ωb)
- densidade de matéria escura fria (Ωc)
- medida do horizonte do som na superfície de último espalhamento (θMC)
- índice espectral das flutuações de densidade (ns)
- profundidade óptica da radiação (τ) e
- amplitude das perturbações primordiais de matéria (∆R).
Os quatro parâmetros seguintes são derivados dos primeiros, não sendo medidos diretamente:
- parâmetro de Hubble (H0= 100h km.s-1.Mpc, em que o índice 0 indica seu valor hoje)
- amplitude das perturbações de matéria em uma escala de 8 Mpc (σ8)
- densidade total de matéria (escura fria + bariônica, Ωm)
- densidade da energia escura (ΩΛ).
Tabela 1 - Lista dos principais parâmetros cosmológicos (adaptado de [2]). Ambas as colunas assumem a cosmologia ΛCDM descrita no texto. A segunda coluna usa os dados de CMB do Planck. A terceira coluna usa dados da segunda coluna combinados com uma compilação de medidas de BAO. As incertezas são mostradas com 68% de confiança.
| Planck TT,TE,EE+lowE+lensing | +BAO | |
|---|---|---|
| Parâmetros "primários" | ||
| Ωbh² | 0,02237 ± 0,00015 | 0,02242 ± 0,00014 |
| Ωch² | 0,1200 ± 0,0012 | 0,1193 ± 0,0009 |
| 100 θMC | 1,0409 ± 0,0003 | 1,0410 ± 0,0003 |
| ns | 0,965 ± 0,004 | 0,966 ± 0,004 |
| τ | 0,054 ± 0,007 | 0,056 ± 0,007 |
| ln(1010∆²R) | 3,044 ± 0,014 | 3,047 ± 0,014 |
| Parâmetros "derivados" | ||
| h | 0,674 ± 0,005 | 0,677 ± 0,004 |
| σ8 | 0,811 ± 0,006 | 0,810 ± 0,006 |
| Ωm | 0,315 ± 0,007 | 0,311 ± 0,006 |
| ΩΛ | 0,685 ± 0,007 | 0,689 ± 0,006 |
A equação (1.1) é um rearranjo das equações de Friedmann-Lemaitre que descreve a combinação dos parâmetros cosmológicos para um Universo com curvatura aleatória. H é a constante de Hubble e k é a constante de curvatura (=0 para um Universo "plano", ou que obedece uma geometria Euclidiana):
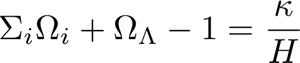
- (1.1)
Os índices i referem-se às diferentes componentes que contribuem para a dinâmica do Universo (matéria bariônica, matéria escura, energia escura, fótons e neutrinos). Observáveis cosmológicos em diferentes redshifts são usados para complementar e validar resultados obtidos com medidas da CMB e montar um quadro mais global da dinâmica e evolução do Universo. A transformação dos observáveis em parâmetros geralmente envolve muitas suposições sobre a natureza dos dados, bem como sobre o "Setor Escuro". Os principais observáveis cosmológicos que são normalmente combinados com dados de CMB são: a) medidas da constante de Hubble em diferentes redshifts; b) Supernovas tipo Ia; c) medidas de BAO em aglomerados de galáxias; d) contagem de aglomerados no meio intergaláctico; e) lenteamento gravitacional fraco.
Além das incertezas estatísticas, incertezas sistemáticas introduzidas em observações com diferentes técnicas podem aumentar muito os erros associados à determinação dos parâmetros. Uma discussão detalhada sobre a física e as estimativas de parâmetros cosmológicos baseados nos observáveis listados acima pode ser encontrado em [3].
Referências
- Planck Collab. (2018) Results VI, arXiv:1807.06209v2
- O. Lahav & A. Liddle. (2019) Cosmological Parameters - a review. arXiv:1912.03687
- D. H.Weinberg; M. J. Mortonson, D. J.Eisenstein; C. Hirata; A. G. Riess & E. Rozog. (2013) Observational probes of cosmic acceleration. Phys. Rep. 530, Issue 2, pp. 87-255